In the 69th minute of the most important derby in English football (that's still the case right?) Manchester United lead Liverpool 1-0 with the game obviously still very much open. An average team in Liverpool’s position would still expect to draw or win the game about 21% of the time, not ideal but nowhere near a lost cause.
With United on the attack and the ball in the final third Carrick plays a weighted ball through to Ander Herrera who latches onto it on the edge of the penalty area. Right here Gomez has a decision to make, he can accept that his positioning wasn't great but just try and track Herrera as quickly as possible, or he can try and redeem himself with a last-ditch tackle near the byline.

Unfortunately for Liverpool Gomez attempted to make up for his poor positional play with a rash tackle on Herrera, fouling him in the process, and greatly diminishing Liverpool's chances of getting anything from the game. It's alright saying it was a stupid decision to dive in with hindsight, but let's try and put a value on the decision Gomez made.
Say there are two different options for a defender in this position, he can either:
- Act aggressively - Attempt to win the ball, or block the ball by sliding in.
- Act conservatively - Stay on his feet and apply as much pressure to the forward as possible without possibility of fouling.
We can have a look at the possible outcomes for each scenario and try and evaluate the value of each action. We're going to define value as the probability of a team scoring from a certain event, adjusting for the possibility of the opposition scoring as a result of the event's outcome when possible.
Aggressive defending: Going to try and split this up into 2:
- Value of a penalty
- Value of every other possible situation
Value of a penalty
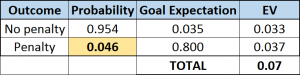
- Penalty given away- in the past 15 years in EPL 80% of penalties have been scored so
Value of a penalty = 0.8
Value of other situations
- Player shoots - Shot conversion from wide penalty areas are converted about 5.6% of the time , more pressure probably reduces this probability, especially if the block rate is higher, so let's say 4-5%
- Player crosses - Let's assume high pressure on cross makes cross more difficult. A cross inside the box is converted about 5% of the time but let’s be generous and say pressure causes value to be about 4%
- Player is tackled before he takes an offensive action - Three things could happen here
- Tackle goes for a corner - 3%
- Offense retains possession - about 2-3%
- Defense obtains possession - 0%
I'm going to assume they all happen at a similar rate and take the average of these at 2% I haven’t got data on the probability that each of these events occur but they're all within range of a value around 2-5%. Based on what seems right, just from a spectators standpoint, I'm going to assume again that these all occur at a similar rate and just find the average to get a value of 3.5%. Obviously I'm making pretty loose assumptions but I'll show why this isn't too important in this particular situation later.
Value of everything else = 0.035
Conservative defending If a defender is conservative the possible outcomes are:
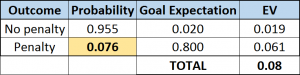
- Player shoots - Shots from this area are converted about 5.6% of the time, let's say 7% when not pressured.
- Player crosses – Crosses in the box are usually converted at about 5% similar to shots from this area, let’s assume slightly more and again say 7% in box when not as pressured
Value of conservative play = 0.07
Since both possible outcomes have about the same chance of conversion the total value is equal to the conversion rate. We are assuming that being conservative makes the opposition twice as likely to score compared to when defending aggressively, I’d like to think this is an assumption which , if biased, is favoured towards aggressive defending.
Expected Value
Okay then let’s do some math. The expected value of each decision is the number of goals the opposition would expect to score given a certain defensive strategy. In this instance (defending) we would want the lowest number possible. So the expected value of playing aggressively is p(0.8) + q(0.035) where "p" is the probability of giving away a penalty, “q” the probability of not giving away a penalty, and therefore p+q=1. The expected value of playing conservatively is 0.07.
From an expected value point of view it only makes sense to defend aggressively if p(0.8)+q(0.035)<0.07, or the chance of the opposition scoring is less than 7%. It turns out that this is only true if “q” (probability of giving up a penalty) is less than 4.6% which seems extremely low. Even if we assume aggressive defending decreases the value of attacking play to 2%, whilst reserved play increases it to 8% you’d need to have a less than 7.6% chance of conceding a penalty in order for being aggressive to make sense. So even when scoring is 4 times more likely when being conservative (which seems pretty extreme), you’d need to be very confident of not fouling in order for this to make sense
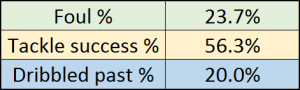
To endeavour to find an approximate value for the proportion of tackles that end up as fouls I decided to collect data for tackles attempted, tackles made, and fouls for premier league defenders over the 2014/15 Premier League season. Now not every foul made is during a tackle, although a foul is an indicator of aggressive defensive play so I decided to include all fouls. With these assumptions I calculated proportion of fouls as.
Foul% = Fouls / (Fouls + Tackles attempted)
This worked out as 23.7% for Premier league defenders last year, Tackle success rate was 56.3% and defenders were dribbled past without committing a foul 20% of the time. From this it’s quite obvious to conclude that defenders should probably never be aggressive in the wide areas of the penalty area since the value of a penalty is far too high to make it worth risking a foul.
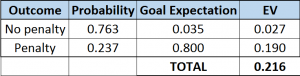
Even if you take into consideration referees swallowing the whistle, meaning refereeing calls are usually given less frequently in high leverage situations or in this case fouls in penalty area, it still doesn't make sense. In order for the foul percentage to fall from 23.7% to less than 7.7% there's got to be some serious whistle swallowing going on. If we go back to our original expected values of 0.8, 0.035, and 0.07, and assume the probability of a foul to be 23.7% we can work out the expected number of goals this would cost a team.
You can see from the table that attempting a tackle in the wide areas of the penalty box on average costs the team 0.146 goals (0.216 - 0.07 = 0.146), which may not sound much, but that’s about half of the goal advantage that an average team playing at home has over the away team.
Managers should be telling their defenders not to dive in or stick a leg out when opposing players are in the wide areas of the penalty box as it never seems to be worth the risk. I think the reason many defenders are too aggressive in this situation is that since defending is reactive compared to attacking being proactive, defenders may feel they need to be risk-seeking in order to make an impact, and in this case it isn't the optimal choice.
It's quite strange that this is the case because teams are usually too risk averse, although maybe attackers are risk averse and defenders are risk seeking, but the proactive attackers have more influence on the game overall, just spitballing but it's an interesting discussion. Just as I was writing this a perfect example of reckless decision making popped up on my twitter feed from the Barcelona vs Rayo Vallecano game, although I'm not even sure if you can class this as decision making.
There are many other situations like this where decision making can be analysed based on expected value and although this may seem like an obvious one from a spectators standpoint defenders still play aggressively in the wide sections of the penalty area. More accurate data will be needed for decisions less obvious than this one but it can still be done and can inform teams where they are losing goals based on decision making. If a team can save themselves .15 goals a game based on simple decisions like this they would save themselves 5.7 goals over the course of the season. In the end that really could be the difference between the club having a successful year and an unsuccessful one.