 For an upcoming IntoPress piece on the ‘confidence’ trope in football, I decided to have a speculative foray into the numbers, drawing inspiration from the ever controversial ‘hot hand’ debate in basketball. That piece, one for a more general audience and with a wider discussion of the topic, will be available to read in a magazine edition released in May. The polarized debate to which I wade into can be caricatured as something like this – in mainstream analysis, ‘confidence’ is often the explanation for what others may often call variance. If Harry Kane is on a poor run of goal-scoring form, missing a shot is a consequence of a lack of confidence, and vice versa. To the other camp, the one I confess to intuitively belonging in, this is largely unproven nonsense. In the end, what I found wasn’t quite what I expected. Method The data used was event level data for the Premier League, La Liga, Bundesliga, Serie A, Eredivisie, Championship, and Ligue 1, as far back as the 2012/2013 season. I grouped the shots by player and season, before adding two extra rolling variables to each of them – ‘confidence5’ and ‘confidence10’, where:
For an upcoming IntoPress piece on the ‘confidence’ trope in football, I decided to have a speculative foray into the numbers, drawing inspiration from the ever controversial ‘hot hand’ debate in basketball. That piece, one for a more general audience and with a wider discussion of the topic, will be available to read in a magazine edition released in May. The polarized debate to which I wade into can be caricatured as something like this – in mainstream analysis, ‘confidence’ is often the explanation for what others may often call variance. If Harry Kane is on a poor run of goal-scoring form, missing a shot is a consequence of a lack of confidence, and vice versa. To the other camp, the one I confess to intuitively belonging in, this is largely unproven nonsense. In the end, what I found wasn’t quite what I expected. Method The data used was event level data for the Premier League, La Liga, Bundesliga, Serie A, Eredivisie, Championship, and Ligue 1, as far back as the 2012/2013 season. I grouped the shots by player and season, before adding two extra rolling variables to each of them – ‘confidence5’ and ‘confidence10’, where:
ConfidenceX = Number of last X shots to have been a goal
This is by no means a perfect proxy for ‘confidence’ – it barely scrapes the surface of the linguistic connotations of the word, but it’s a starting point. It rolls between games, and so is slightly less vulnerable to score effects and game states, but not seasons. A shot taken by a player who had taken less than 5 or 10 shots in that season would get a Confidence5/10 score of ‘0’. I also randomly ordered the same set of shots and created the same variables in order to have a control group. Aggregating by ‘confidence’ score and looking at average conversion rates, I was then able to test for any discernible linear relationship between the two. Applying Pearson’s Product-Moment Correlation and t-tests at a significance level of (< 0.05), ‘confidence5’ strongly correlated with conversion and in a statistically significant manner, while ‘confidence10’ correlated weakly but without significance. Immediately sceptical of the ‘confidence5’ correlation, I ran the same calculations on the control group; at the rolling 5-shot level, it correlated fairly strongly, but without any statistical significance (p-value ~ 0.2). Nonetheless, I was concerned about sample size issues - in the whole dataset of shots, there were only 16 streaks of 5 goals from the 5 preceding shots, and some of these are the same player in quick succession: in two matches against Hertha Berlin and Werder Bremen last season, Bas Dost managed to take a shot having scored his last five 3 times. In light of this, I filtered out any chances under 0.2 expected goals by my model and ran the same correlation tests – now, for a streak of 5, there were 150 examples (which still isn’t great). At the rolling 5 shot level, the correlation became even stronger and more significant (p-value ~ 0.02). With ‘confidence10’, the relationship was still not significant enough (p-value ~ 0.26) to reject the null hypothesis that it has no bearing on conversion. In terms of the possible effect being observed, this strengthens the possibility of a short-run ‘hot/cold feet’ phenomenon – if this was just picking up player quality, where players who score more will score more, it would probably be significant at the rolling 10-shot level too. Applying the same filter and method to the control group, neither the 5 or 10 level was significantly correlated with conversion. As another check, I looked at the relationship between a shot in the sample’s xG and the average xG of the 5 shots before it – if this was high, any ‘hot feet’ effect could just be a proxy for the repeatability of chance quality at this micro level. As it turned out, they were correlated positively and significantly, but probably too weakly (correlation coefficient of ~ 0.014 by Pearson’s) for this to be the case. Perhaps there really was an effect here. 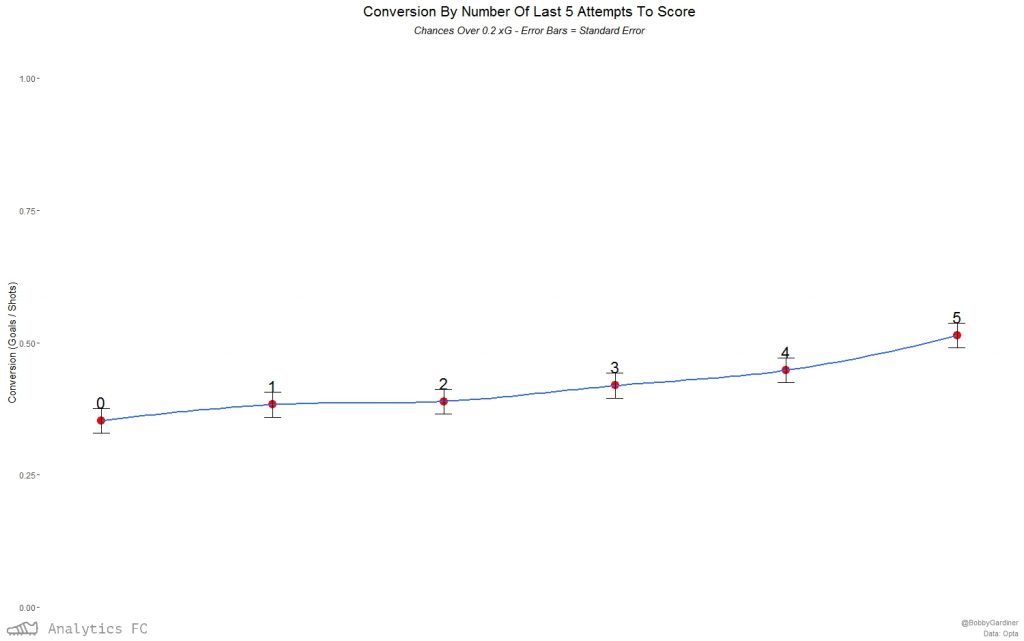 The relationship seems to apply to xG conversion too.
The relationship seems to apply to xG conversion too. 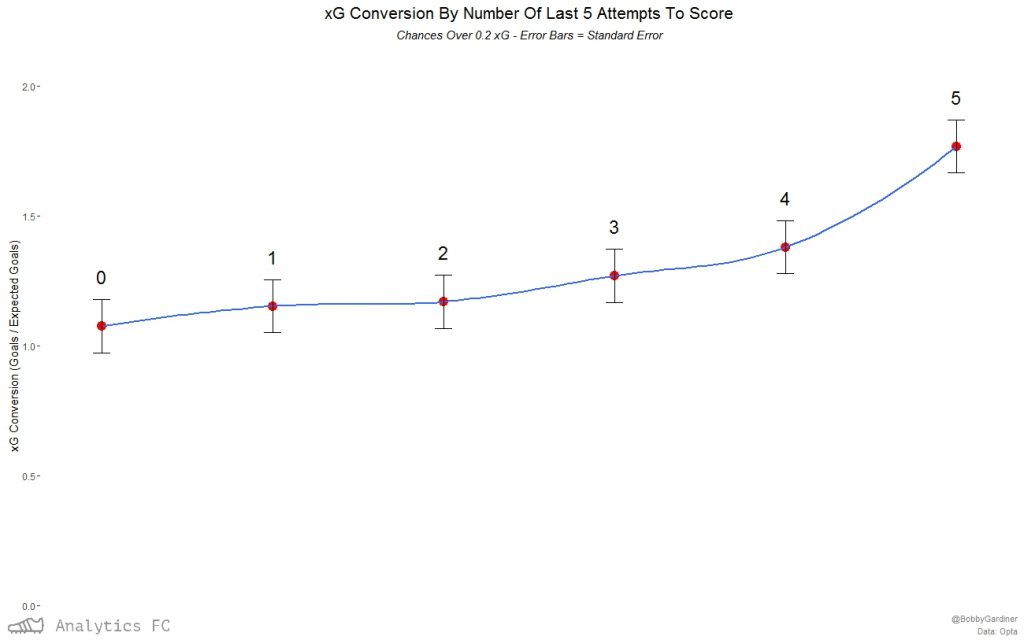 Again, this isn't the case for the control group.
Again, this isn't the case for the control group. 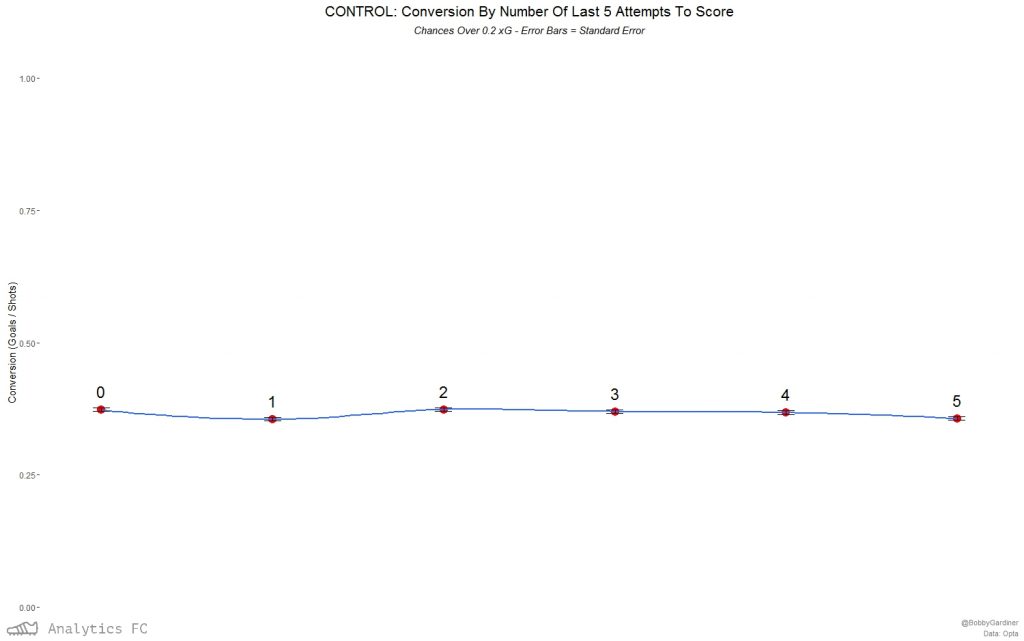 Going back down to the event level data with a logit regression for all chances over 0.2 xG, again the number of the last 5 chances scored was a significant factor in affecting the probability of one of these chances going in. Predicting the probability of success with this model based on ‘confidence5’ alone, I can then plot the relationship with 95% confidence intervals. The model has a McFadden pseudo-r2 of ~ 0.0022 (these tend to be “considerably lower” than OLS r2s in McFadden’s own words), and so is expectedly a small effect.
Going back down to the event level data with a logit regression for all chances over 0.2 xG, again the number of the last 5 chances scored was a significant factor in affecting the probability of one of these chances going in. Predicting the probability of success with this model based on ‘confidence5’ alone, I can then plot the relationship with 95% confidence intervals. The model has a McFadden pseudo-r2 of ~ 0.0022 (these tend to be “considerably lower” than OLS r2s in McFadden’s own words), and so is expectedly a small effect. 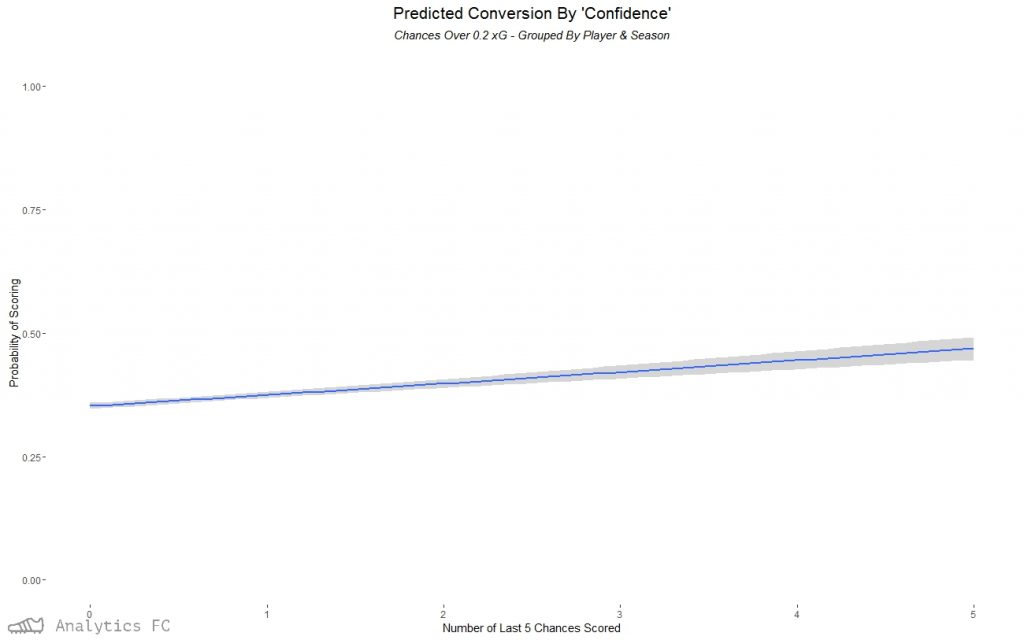
| Confidence | Predicted Probability of Scoring |
| 0 | 0. 3521575 |
| 1 | 0. 3745545 |
| 2 | 0. 3975019 |
| 3 | 0. 4209090 |
| 4 | 0. 4446772 |
| 5 | 0. 4687013 |
According to this, a chance (over 0.2 xG) preceded by 2 goals in the last 5 chances would have roughly a 4% higher chance of going in than one preceded by none. This is loosely equivalent to the difference between taking a shot from 15 metres out and 10 metres out, all else equal. If all 5 had been scored previously, it would predict roughly an 11% higher chance. I would be surprised if the effect was this large and this linear - as can be seen from the larger confidence intervals towards the higher confidence levels, uncertainty is an issue with the decreased sample size of larger streaks. Conclusion Although a small factor, one fairly tiny in terms of affecting the probability of scoring compared to, say, location, a ‘hot feet’ style effect may very well exist in the short run for non-terrible chances. The logical next step is to look at rolling expected goal over-performance as a predictor of shot success - I had a quick look at this and it got very complicated very quickly. My methods are likely to be imperfect as a second year undergraduate, and like all endeavours in football stats, this is probably going to be complicated by systemic biases. As ever, I’m still sceptical, and so defer to the more capable and qualified to shoot this down. If you have any ideas about a way to improve the methodology or completely up-end it and test the theory in another way, I’m more than happy to talk about it: @BobbyGardiner.