In my last entry I pledged to answer this question using the 'repeatability' methodology I presented there. This will be a quick entry to confirm that luckily, we've been right all along and 3 is the ideal length to consider for passing motifs. The number of passes considered in a passing motifs analysis is a clear instance of the trade-off between detail and comparable structure that we discussed in the previous entry. The Figure below shows the number of motif types that occurred in the 2015-16 season of the Premier League depending on the number 'k' of passes we choose as 'length' from 3 to 7: 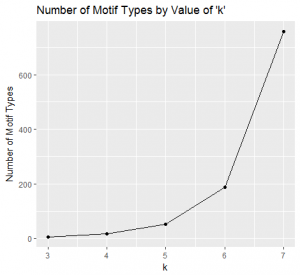 When we choose to consider 3 passes, there are 5 motif types which I hope all my readers know by heart by now: ABAB, ABAC, ABCA, ABCB and ABCD. If we choose to go up to 4 and consider one extra pass, there are 15 different types: ABABA, ABABC, ABACA, ABACB, ABACD, ABCAB, etc. For 5-passes long motifs there are 52 types (all of which occurred at some point in the 2015-16 season), and for 6-passes long motifs there are 203 (of which only 187 types occurred in the 2015-16 data). There were 759 different types of 7-pass motifs in the data. We can appreciate how the number of motif types grows quickly with the number of passes we are considering, which precisely lends itself to losing structure in the noisy haze of excessive detail. The Figure below shows the number of motifs for the 2015-16 season for each number of passes 'k' considered:
When we choose to consider 3 passes, there are 5 motif types which I hope all my readers know by heart by now: ABAB, ABAC, ABCA, ABCB and ABCD. If we choose to go up to 4 and consider one extra pass, there are 15 different types: ABABA, ABABC, ABACA, ABACB, ABACD, ABCAB, etc. For 5-passes long motifs there are 52 types (all of which occurred at some point in the 2015-16 season), and for 6-passes long motifs there are 203 (of which only 187 types occurred in the 2015-16 data). There were 759 different types of 7-pass motifs in the data. We can appreciate how the number of motif types grows quickly with the number of passes we are considering, which precisely lends itself to losing structure in the noisy haze of excessive detail. The Figure below shows the number of motifs for the 2015-16 season for each number of passes 'k' considered: 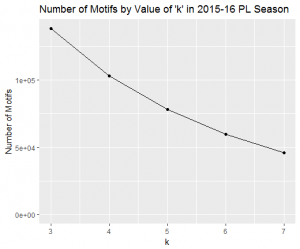 There were 138,432 3-pass long sequences compared to 45,820 7-pass long sequences. While there is a considerable amount less, the data set is still of a decent size to believe that we can extract meaningful conclusions. Finally, the figure below shows the repeatability percentage as per the methodology of the previous entry for each choice of length from 3 to 7 (as before, we consider relative frequencies of the different categories rather than raw amounts):
There were 138,432 3-pass long sequences compared to 45,820 7-pass long sequences. While there is a considerable amount less, the data set is still of a decent size to believe that we can extract meaningful conclusions. Finally, the figure below shows the repeatability percentage as per the methodology of the previous entry for each choice of length from 3 to 7 (as before, we consider relative frequencies of the different categories rather than raw amounts): 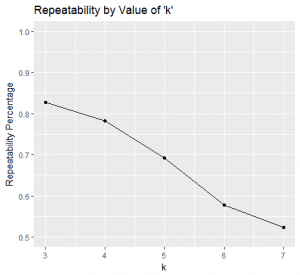 3-pass long motifs have a repeatability of about 82.7%; while 6 and 7-pass long motifs have 57.8% and 52.3% respectively. Considering that as per our methodology random methods that carry no structure would have 50% repeatability (equivalent to randomly assigning style), these figures mean that by then we've lost almost all structure. It's an interesting conclusion that sequences of 3 passes are the ideal number to consider which carry unique team structure better than longer sequences. Considering that passes constitute the grand majority of events on a football pitch, it's a far-reaching conclusion. It provides insight into breaking down the sequentiality of football matches into representative constituent blocks: looking at blocks of about the size corresponding to 3 passes should be best practice.
3-pass long motifs have a repeatability of about 82.7%; while 6 and 7-pass long motifs have 57.8% and 52.3% respectively. Considering that as per our methodology random methods that carry no structure would have 50% repeatability (equivalent to randomly assigning style), these figures mean that by then we've lost almost all structure. It's an interesting conclusion that sequences of 3 passes are the ideal number to consider which carry unique team structure better than longer sequences. Considering that passes constitute the grand majority of events on a football pitch, it's a far-reaching conclusion. It provides insight into breaking down the sequentiality of football matches into representative constituent blocks: looking at blocks of about the size corresponding to 3 passes should be best practice.
2017
What's the ideal length of passing motifs?
By admin
|
April 13, 2017
