The consensus in the football analytics community appears to be that finishing skill exists, but is only provable given large samples of shots, and hence estimation of this skill for individual players is impossible at worst and problematic at best. The debate took place in 2014: among others, Michael Caley showed that advanced players convert equivalent chances better than the more defensive ones (and later incorporated a player adjustment in an xG model), and Devin Pleuler demonstrated weak year-on-year repeatability of superior shot placement. Mike Goodman neatly summarised the conceptual pitfalls of talking about "finishing skill"; here I use this term in the "outperforming xG" sense. More recently (and most relevantly to the work described below), Sam Gregory showed a basic Bayesian approach to estimating players' personal conversion rates.
Each of these studies has its merits but, especially looking back from 2017, each is methodologically suboptimal. I say this not to take shots at old work -- my own was no better at the time -- but to argue for a better, more complete and more powerful approach to the problem.
To run through these issues quickly: Michael didn't analyse individual skill at all but looked at aggregates beyond the player level, meaning that his approach can't tell you much about one player of interest versus another. Devin's work was a victim of the contemporary epidemic of repeatability studies, that is using a correlation or lack thereof between season-on-season values of a metric as the indication of whether the metric contains signal. I have argued against this setup in private many times, but it's time to say publicly that while repeatability as an objective is good, repeatability as a methodology is bad.
In a low-sample sport like football, we need to wring every little bit of info from every datapoint, so it is unconscionable to start analysis by halving the sample size. Fortunately, the analytics community appear to have recognized that collectively, and I have not seen many repeatability studies recently. Lastly, Sam's work is closest in spirit to what follows, but since it was done without accounting for chance quality (ie. xG), we see poacher types topping his list (and Messi; there's always Messi), in large degree due to their chances being best on average rather than due to individual ability.
My own answer to the finishing skill question is that it not only obviously exists, but it also leaves a measurable trace in small samples of shots. In fact, I was able to show that for many players, including superstars as well as relative unknowns, the probability that they are above-average finishers is very high. Furthermore, even if estimation of the skill of individual players is fraught with uncertainty, quantifying this uncertainty is not only part of our job as analysts, but can itself be an essential contribution, allowing the decision-makers to consume model results in line with their appetite for risk.
METHODOLOGY AND RESULTS
My approach is an xG model where the identity of the player is a factor, and I interpret the player-specific coefficients as a measure of the player's finishing skill. Of course, if done naively, this would go horribly wrong: the players who have taken very few shots and converted them all by chance would emerge as prime finishers. (There are also computational pitfalls to the naive approach which I won't go into here.)
Hence, it is imperative to not only quantify the uncertainty of the skill estimates, but that the estimates themselves are, loosely speaking, shrunk towards the mean in proportion to how many observations there are for the player. And for that, we need to move beyond fixed-effect regressions. In this article I employ Bayesian inference; for a very gentle and practical introduction to this subject I can recommend the second edition of John Kruschke's book "Doing Bayesian Data Analysis".
The complete code for this project is available at https://github.com/huffyhenry/statsbomb-bayesian-shooting/ under the GNU LGPG v3 licence. The dataset that I used consists of 182'288 non-penalty shots from the big 5 European leagues, from 2010/11 onward. These shots were taken by 3906 distinct players, with individual sample size typically less than 100; in fact, only 150 players recorded more than 200 attempts, and only 5 (Cristiano Ronaldo, Messi, Suarez, Lewandowski and Higuain) more than 500. The model itself is a fairly basic logistic regression, taking distance to the center of the goal, visual angle of the goal and several binary features, as well as the player's identity, as predictors. I specified this model in JAGS, which is a Bayesian inference engine.
By performing laborious computations, JAGS is able to distribute the credit for scoring between the player and the circumstances of the shot in the optimal way. Most still goes to the shot's properties, and in that this model is not that much different from the typical, player-agnostic xG models; in fact, it should recover (approximately) the coefficient values obtained by running a classical, player-agnostic logistic regression on the same data. But some of the credit for scoring (or penalty for missing) accrues to the players, and it is the estimates of these player-specific variables that are the main output of this model.
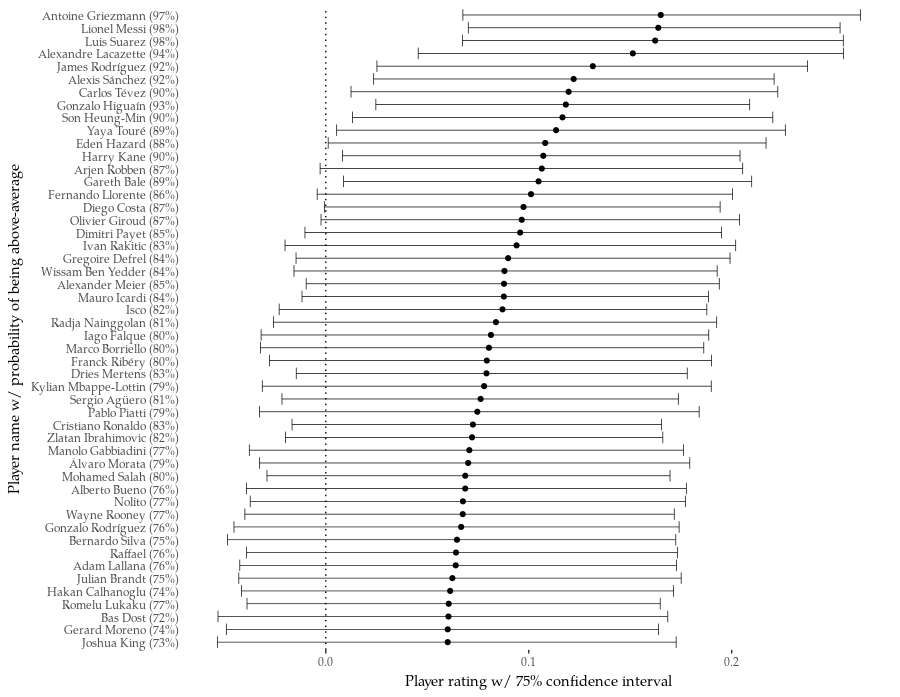
The graph above shows the best 50 finishers according to the model. The dot marks the estimate of player's skill; because of the structure of the model, these numbers do not have a direct interpretation in football terms, but higher is better, and 0 means an average finisher. The error bars mark the interval in which the player's skill lies with 75% probability. Lastly, the probability that a player is an above-average finisher is given in brackets after his name. To run quickly through this list: the top is very satisfying, composed almost entirely of pre-eminent strikers of our age.
Long shot merchants are conspicuously well represented too. Shockingly (to me at least) 57 shots were enough for Kylian Mbappe to break into top 30. In a sanity check that all shooting models must pass, Jesus Navas is in the bottom 10. Of notable absentees on the Top 50 list, Pierre-Emerick Aubameyang is around 250th (62% probability of being above-average), Klaas-Jan Huntelaar is ~330th (60%) and Robert Lewandowski ~550th (56%) -- all with positive skill estimates, but with CIs comfortably overlapping zero.
And so we arrive at the elephant in the room: out of almost 4000 players, only a handful have skill different from 0 at the 75% confidence level. Does it mean that, as long been suspected, looking for individual finishing skill in the data is a fool's errand? No. If you are a director of football tasked with signing a good finisher, you should not ignore a model signal at the 75% level (and in fact for many players the confidence in their above-average skill is higher, since the model may be underestimating it).
Picking one of the top but available names, like Roma's and Arsenal's new buys, would be entirely justified as a calculated gamble, seeing how the probability that they are not above-average finishers is very low. Second, in part to keep this analysis manageable and in part because I had only this data on hand, I limited myself to the Big Five over the last few seasons. Including second division data for these five countries, feeder leagues like the Eredivisie, as well as the Champions and Europa Leagues would significantly boost sample sizes for many players and shrink their CIs.
DISCUSSION
Let's discuss the shortcomings of this analysis now. Enamoured as I am with explicit modelling of uncertainty and with the ability to treat players very much like first-class citizens of the model, the analysis is problematic for several reasons, to the point that I would not recommend direct application of this implementation in scouting. The main issues in a rough order of importance are as follows:
First and foremost, my model knows nothing about shot placement and force. Arguably, players should receive credit for hammering their shots towards the corners of the goal, even if these shots are saved, and should be penalised for shooting tamely towards the center of the goal -- perhaps even if they do score. I would expect placement and force to not only change the results of this analysis in terms of the top 50 list, but also to contain enough information to push the estimates for many players further away from the 0 line, ie. bring about much more confidence into the assessment of individual players. After all, this was the main take-away from Devin's article. In the same vein, an industrial-grade model should include the goalkeepers as well.
Second, the xG model I used here is relatively basic. If it consistently underestimates the quality of the chances falling to a particular player, then this player is going to incorrectly receive extra credit for converting them (and be unfairly penalised in case of overestimation). This is a milder version of the problem with Sam Gregory's analysis. On the other hand, certain circumstances that we normally think of as being shot descriptors can also be viewed as part of the player's finishing, and should not be included in the underlying model; this is why I don't tell the model whether the shot follows a successful dribble by the player. Lastly, the ~200k sample used to build the model is also not as big as it could be, perhaps leading to incomplete separation of player and shot circumstance effects for some rarer on-pitch situations.
Third (this is a bit technical), the skill is conceptualised as an additive boost to the linear predictor in a logistic regression. If you recall the shape of the logistic function, it becomes clear that adding a fixed value (ie the skill) to the argument can have a radically different effect on the outcome depending on the argument value.
More precisely, adding a fixed quantity to a very low or very high value has a smaller effect than adding to a value near 0, where the function value changes the sharpest. But 0 corresponds to shot xG of 0.5, which is very very high in the wild, so we can ignore the high end. Thus, if players A and B consistently convert at double their xG, but player A's average xG/shot is higher than player B's, then the model will estimate A's finishing skill as lower than B's.
This effect may explain the strong presence of long distance shooters on the top 50 list, and partially also Rodriguez' high place. Having the skill term enter the predictor in a different way could alleviate the problem to a degree.
Fourth, the Bayesian prior on shooting skill that I used is arbitrary (0-centered normal with 0.01 variance), and in the small-sample environment that we have here, the selection of priors has considerable impact on the final results.
In an earlier version of this analysis, I used a much less committal prior, which resulted in a few odd names creeping up the list purely because they converted a large proportion of their relatively few chances and the model had to price in the possibility that they possess superhuman finishing ability. I believe that the model would benefit significantly from a set of priors that better reflect our beliefs about finishing, but that is difficult because, as discussed above, the skill variable has no direct interpretation.
Fifth, the model assumes single finishing skill for a player, when I can think of at least four distinct skills: stronger foot, weaker foot, head and long range. It would make sense to at least remove the headers from the dataset, even though the eye test and some anecdotal evidence suggests that head and foot finishing skills are correlated.
But what the plots above make reasonably clear is that subdividing the shots into even smaller samples is going to make the CIs balloon, unless perhaps in the rarer cases where the player is above-average finisher of one kind and below-average of the other. One thing that could help a little would be to include the information whether the shot was taken with the weaker foot as a single covariate (ie shared by all players), but I don't have foot preference data.
EPILOGUE
Bayesian models are powerful and intuitive, but they do have practical drawbacks. The leading Bayesian inference engines require specifying the model in their own domain-specific languages inspired by these ideals of elegance and succinctness that are C++ (Stan) and R (JAGS). Fitting these models on datasets of typical size in football analytics, ie. hundreds of thousands of datapoints, takes hours if not days.
And assessing convergence of the model requires an uncomfortably deep understanding of MCMC techniques. For these reasons, I have replicated this analysis using Generalized Linear Mixed Model (GLMM) framework from the R package lme4, specifying the usual xG model predictors as fixed effects and players as random effects. The code for this analysis is also included in the repository above. The encouraging news is that the skill estimates between full Bayes and GLMM are very highly correlated. Since both models estimate the same model, the agreement cannot be taken as validation of my analysis; but it does suggest very strongly that GLMMs are a valid, scaleable alternative to full Bayes.
I am indebted to Will Gürpınar-Morgan, Martin Eastwood, Devin Pleuler, Sam Gregory and Ben Torvaney, who read an earlier version of this article and provided feedback which improved it considerably. Łukasz Szczepański taught me how to use GLMMs to study players, and Thom Lawrence inspired me to get serious about Bayesian inference. The data used in the article was collected by Opta.
In 2018, StatsBomb started collecting our own proprietary data set that introduced many new features to the industry, including defender and goalkeeper locations on shots, shot impact height, pressures, and pass height and footedness information. If you'd like to know more, contact us today.
