Based on this year’s figures, Luis Suarez is an exceptional goal scorer. Daniel Sturridge less so…!
[Dramatic pause for effect.]
Now that the bomb is away, let’s focus on the stats.
This article is written to explain how one could compare what was expected to happen (based on some statistical model) and what actually happened, and how to quantify how likely that result was, in the end. It may appear to somewhat overlap with my previous article on the statistical significance of comparing metrics, but it should be stressed that both pieces have been written to illustrate methods, using data for demonstration rather than to focus on the particular data analysed.
Goal expectation (ExpG) models have been growing like mushrooms in the football analytics community. Some analysts have published the details of their models; others have kept the calculations to themselves. In general, these models take into account a number of factors affecting the probability of a shot being scored and assign a numerical “goal expectation” value to each shot. This way, one can assess the performances of players in terms of scoring by comparing the actual number of goals scored compared to what would be expected given the nature of the chances they took.
This article is partly motivated by this post by Mark Taylor in which he indirectly highlight the fact that knowing the total ExpG figure of each player/team is not sufficient, but one needs to know how that ExpG breaks down i.e. the ExpG value of each shot. The reason behind this is that the distribution of the ExpG figures will affect the probability of scoring 0, 1, 2, … goals etc.
Armed with this, I’ve set about to check how the number of goals actually scored by a player compares to what was expected from him, given the chances he took. I’ve used the goal expectation model that was developed by Colin Trainor and myself, introduced in this piece and whose results have been used on this site.
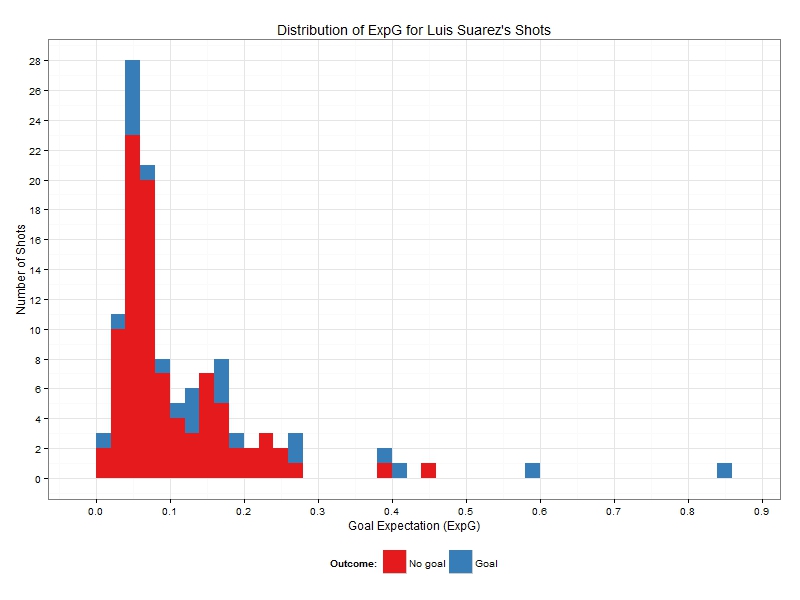
Let’s start with the Premier League top scorer. The following chart depicts a histogram of the ExpG of his shots:
More than 50% of his shots have an ExpG figure between 0.02 and 0.08. A few of his shots arise from even more difficult chances but there are some shots from relatively good positions including a couple which he was odds-on to score (and he did). I should note here that other analysts may have different numbers depending on how their models calculate ExpG, but that is not that important right now as the same theory applies but the results may differ slightly (I presume).
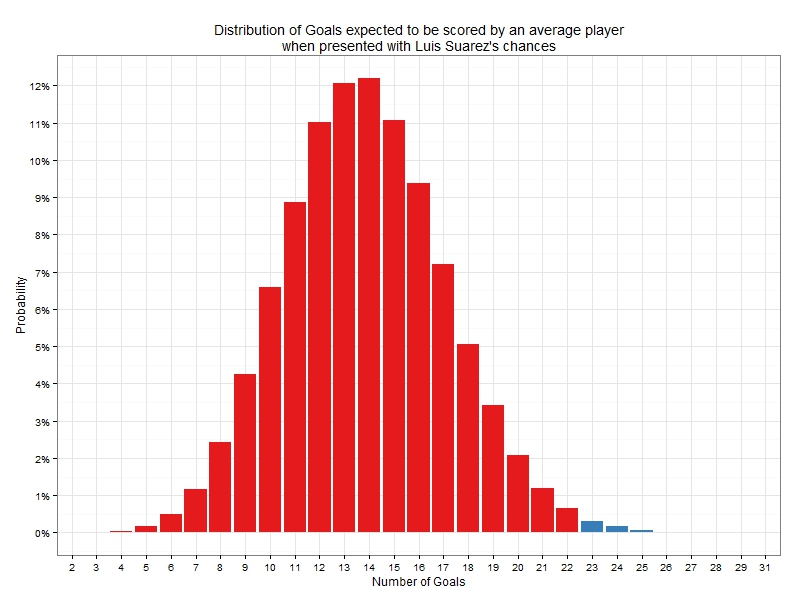
Based on our results, the total ExpG figure for Suarez’s 116 shots was 13.8 goals. Instead, he found the net a total of 23 times. If we assume that the ExpG figure assigned for each shot closely resembles the goal expectation of that particular shot from an average player, we can calculate the probability of a player actually scoring 0 goals out of 116 similar shots to the ones taken so far by Suarez. That would be given by:
Prob( 0 goals ) = ( 1 - ExpG_1 ) * ( 1 - ExpG_2 ) * …. * ( 1 - ExpG_116 ) = 0.0000000653 = 0.00000653%
where ExpG_i is the goal expectation of the ith shot. Similarly, we could calculate the probability of our average player scoring 116 goals which would be:
Prob (116 goals) = ExpG_1 * ExpG_2 * … * ExpG_116 = 0.000 … (total of 124 zeros!) … 000217
Obviously, both probabilities are very small. We could sit down and write down algebraic expressions for the probability of the average player scoring 1, 2, 3, …, 114, 115 goals too. [For the statistically-oriented readers, that is the probability distribution of the sum of 116 Bernoulli variables which don’t necessarily have the same success probabilities (given by ExpG_i in each case here)]. Instead of doing that, we can simulate these shots/goals and look at the resulting distribution. Out of the 116 shots Luis Suarez took, the average player would score goals with the following distribution:
As designed, the average would be 13.8 goals, but inspecting the whole distribution is much more revealing. The probability of an average player scoring 23 goals or more (i.e. equaling or surpassing Suarez performance) is just 0.6% and is highlighted in blue in the chart above. This indicates how exceptional Suarez’s goal scoring performance has been this season.
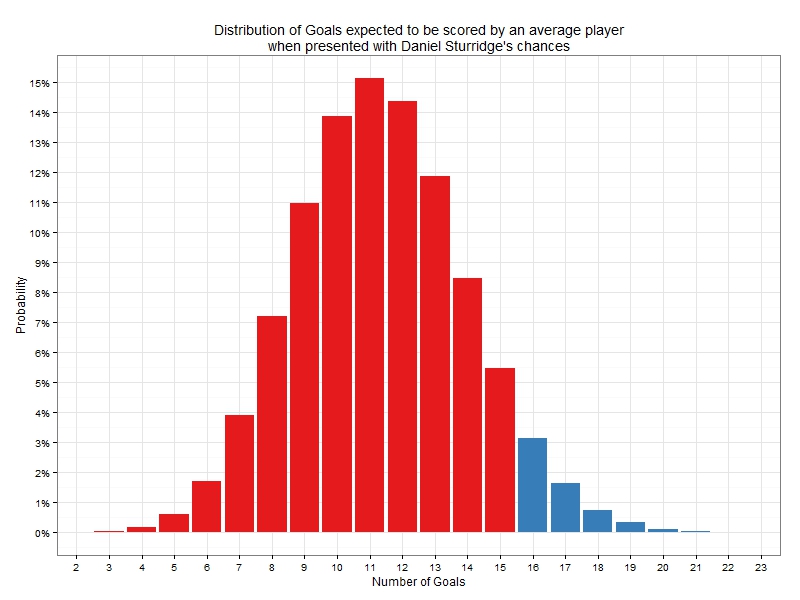
If we repeat this process for Daniel Sturridge and his 63 shots the goal distribution is as follows:
The probability of an average player equaling or surpassing Sturridge’s tally of 16 goals given the chances Daniel took is 6.1%. It’s still low, but not as impressive as Suarez’s.
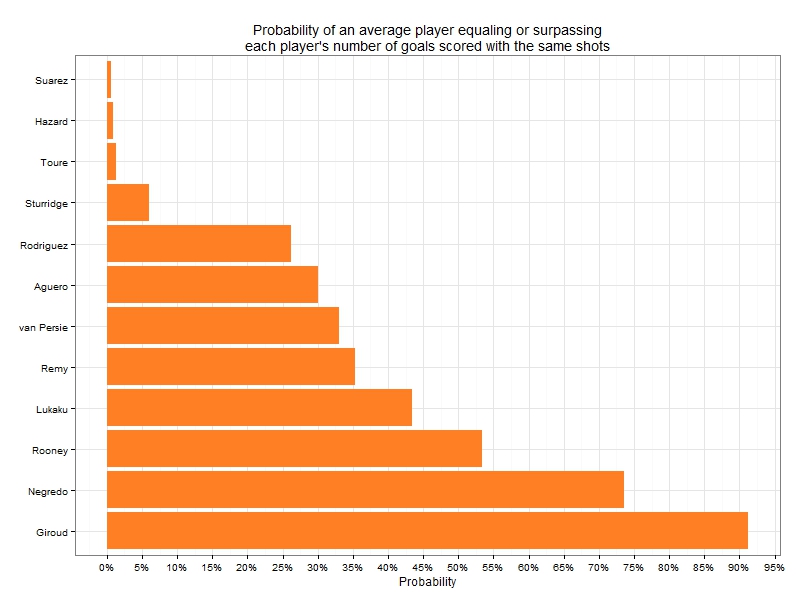
I’ve carried out the same analysis for all players who scored an arbitrarily chosen number of 9 or more goals in the Premier League so far this season and calculated the probability that an average player would equal or exceed the observed performance (i.e. the number of goals scored) of each player. Note that the penalty goals (or misses) need not be removed from the simulation, as they have been assigned a higher ExpG value which reflects the goal expectation of those shots. The resulting probabilities are shown in increasing order in the following chart:
If we were to use the 5% significance level, only 3 players (Suarez, Hazard and Yaya Toure) have demonstrated statistically significant, above-average, goal scoring performances once the nature of their chances has been taken into consideration. They are followed by Sturridge who narrowly misses the cut. However, the remaining leading goalscorers have not demonstrated any exceptional ability in converting their chances and in fact, players like Giroud and Negredo have been vastly underperforming in terms of the number of goals they actually scored compared to the number they were expected to contribute given the chances they took. Especially, in Giroud’s case, the 10 goals scored compared to the 13.6 he was expected to score given his chances, constitutes serious underperformance which suggests that perhaps Arsenal should be looking for reinforcements in that area in the summer.
As a concluding remark, I’d reiterate that this is a method to compare actual versus expected goals scored which does not make any unnecessary distributional assumptions on ExpG. It can therefore accommodate comparisons either in terms of specific players who could have a non-homogeneous shot profile (e.g. including shots from favourable positions, penalty shots or long range attempts) or even be used to evaluate a team’s scoring performance. Finally, it can be applied from a defensive standpoint to evaluate how teams or goalkeepers have prevented shots from being scored.